Le bruit blanc

Centre d'Études et de Recherches

sur les Phénomènes Inexpliqués

Le bruit blanc

Le bruit blanc est un "phénomène", pour autant que l'on puisse l'appeler ainsi, tout ce qu'il y a de plus courant, accessible sans aucun problème et aussi apparemment sans la moindre utilité... Nous l'étudierons toutefois avec attention car il est particulièrement important en TCI (transcommunication instrumentale), soit l'un des moyens "technologiques" pour communiquer avec l'au-delà. En 2008, le CERPI n'avait pas encore investigué réellement à propos de la TCI. L'un de nos correspondants avait toutefois assisté à certains ateliers qui s'étaient déroulés à Verviers, notamment avec les parents de Karine Dray (Karine après la vie). Fin 2008, une personne nous contacta pour une affaire qui allait être l'élément déclencheur des opérations. Le CERPI allait donc "prendre le train en marche", mais - comme d'habitude - il allait aussi se comporter comme un TGV pour rattraper son retard et se positionner dans le peloton de tête...

Définition

Nous allons rapidement voir que les scientifiques ont le chic pour tout compliquer et que d'un phénomène apparemment très simple, on obtient des démonstrations extravagantes, comme celles que l'on voit sur les tableaux des savants fous, dans certains films d'anticipation. La réalité est pourtant toute simple, nous l'avons dit : un bruit blanc est une réalisation d'un processus aléatoire dans lequel la densité spectrale de puissance est la même pour toutes les fréquences. Vous voyez ci-contre un échantillon de bruit blanc à l'oscilloscope. On parle souvent de bruit blanc gaussien, il s'agit d'un bruit blanc qui suit une loi normale de moyenne et variance données. En synthèse et traitement du son, on ne considère que les fréquences comprises entre 20Hz et 20kHz puisque l'oreille humaine n'est sensible qu'à cette bande de fréquences (la sensibilité varie toutefois selon les personnes). L'impression obtenue est celle d'un souffle. Le son produit lors de l'effet de «neige» sur un téléviseur déréglé est un bon exemple de bruit blanc.

Hé bien... nous y voilà donc ! Un bruit blanc ce n'est donc pas plus compliqué que ça, c'est ce bruit caractéristique que l'on obtient lorsque, par exemple, on positionne le curseur de recherche d'une radio très classique (et peu sophistiquée) entre deux "stations". On ne reçoit bien évidemment aucune émission, strictement rien d'intelligible a priori, rien que du "brouillard" un truc qui fait "pshhhht". On peut aussi comparer cela à certains écrans que vous obtenez sur votre télévision lorsque vous essayez de programmer un appareil auxiliaire, par exemple un magnétoscope. Seulement voilà, la définition scientifique s'accommodant mal de "pshhhts", il était nécessaire d'utiliser des termes plus appropriés, raison pour laquelle on a eu recours à la densité spectrale de puissance, et là, c'est moins marrant. Comme on ne peut pas raisonnablement expliquer quelque chose on ayant recours à des termes qu'il faut expliquer, expliquons donc les termes compliqués qui tentent d'expliquer les premiers (euh... si vous nous suivez !):

On définit la densité spectrale de puissance (DSP en abrégé, Power Spectral Density ou PSD en anglais) comme étant le carré du module de la transformée de Fourier. Ainsi, si x est un signal et X sa transformée de Fourier, la densité spectrale de puissance vaut Γx = | X | 2. (Tout le monde s'en doutait et personne n'osait le dire, n'est-ce pas ?) Bon ! Là dessus, oserions-nous nous demander ce qu'est la transformée de Fournier ? Oui, bien sûr ! Osons-le donc et laissons ce soin à Wikipédia : http://fr.wikipedia.org/wiki/Transform%C3%A9e_de_Fourier pour ce qui est d'y répondre. Bref, ne nous dispersons pas, il va déjà falloir s'accrocher ! Revenons donc à notre densité spectrale de puissance et à son autocorrélation.

Densité spectrale de puissance et autocorrélation

La définition de la fonction d'autocorrélation temporelle d’un signal x à temps continu est :

\gamma(\tau)=\int_{-\infty}^{+\infty}x^{*}(t)x(t+\tau) \, dt

où * est la conjugaison complexe.
Prise au point τ, cette fonction mesure en quelque sorte la manière dont les structures que l'on peut voir dans un signal se répètent sur des échelles de temps de l’ordre de τ.
Sa définition à l'aide de l'opérateur de convolution est :

\gamma(\tau)=x \ast x^*(-)

Les propriétés de la transformée de Fourier impliquent que la densité spectrale est la transformée de Fourier de l'autocorrélation :

\mathcal{F}[\gamma]=\mathcal{F}[x] \times \mathcal{F}[x^*(-)]=X \cdot X^*=\Gamma

Calcul détaillé

Calculons sa transformée de Fourier Γ(ν):

\Gamma(\jmath\omega)=\int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty}x^*(t)x(t+\tau)e^{-\jmath\omega\tau}\, dt \, d\tau, '\jmath' désignant le nombre complexe de carré égal à -1.

Cette expression peut se mettre sous la forme :

\Gamma(\jmath\omega)=\int_{-\infty}^{+\infty}\left(\int_{-\infty}^{+\infty}x(t+\tau)e^{-\jmath\omega(t+\tau)}d\tau\right)x^*(t)e^{+\jmath\omega t} \, dt

On effectue dans l'intégrale centrale le changement de variable u=t+τ et il vient :

\Gamma(\jmath\omega)=\int_{-\infty}^{+\infty}\left(\int_{-\infty}^{+\infty}x(u)e^{-\jmath\omega u}du\right)x^*(t)e^{+\jmath\omega t} \, dt

Soit encore :

\Gamma(\jmath\omega)=X(\jmath\omega)\int_{-\infty}^{+\infty}x^*(t)e^{+\jmath\omega t} \, dt

On effectue le changement de variable u=-t et on obtient :

\Gamma(\jmath\omega)=X(\jmath\omega)\int_{-\infty}^{+\infty}x^{*}(-u)e^{-\jmath\omega u} \, du

On reconnaît, dans le deuxième terme, la transformée de Fourier de x*(-t). Or la transformée de Fourier de x* vaut X*(-ν), et la transformée de Fourier de x(-t) vaut X(-ν). Le deuxième terme vaut donc X*(jω), donc Γ(jω)=X(jω)X*(jω)=|X(jω)|2: la densité spectrale de puissance est aussi la transformée de Fourier de l'autocorrélation.

Les amoureux des formules, les matheux et autres fervents des expressions symboliques étant à présent rassasiés (du moins nous l'espérions), venons-en à des considérations plus pratiques. Car enfin, à quoi tout cela va-t-il bien pouvoir nous servir ? (D'autant que nous avions stipulé en avant-propos que cela ne servait à rien ! Hé bien, figurez-vous que, contrairement aux apparences, il va falloir revoir sa copie à ce sujet ! Et pas qu'un peu !)

Utilisation de la densité spectrale de puissance dans les télécommunications

En télécommunications, on doit souvent traiter des signaux aléatoires. Cependant, on ne peut calculer la transformée de Fourier d’un signal non entièrement connu. En revanche, on peut calculer l’autocorrélation d’un signal aléatoire connu par ses propriétés statistiques. La densité spectrale de puissance est donc, souvent, utilisée en télécommunications.

Considérons, par exemple, le «bruit blanc». Le bruit est un exemple type de signal aléatoire. La valeur du bruit, à un instant donné, n'est absolument pas corrélée avec la valeur du bruit aux autres instants. Cela se traduit par une fonction d'autocorrélation du bruit égale à une impulsion de Dirac (c'est-à-dire égale à l'infini en 0, et 0 ailleurs, comme chacun sait). La transformée de Fourier d'une impulsion de Dirac est la constante unité (le module vaut 1 quelle que soit la fréquence). On définit alors, par «bruit blanc», un bruit dont la densité spectrale est constante suivant la fréquence. En télécommunications, on considère souvent les bruits comme étant blancs, tout du moins dans les bandes passantes des systèmes étudiés. 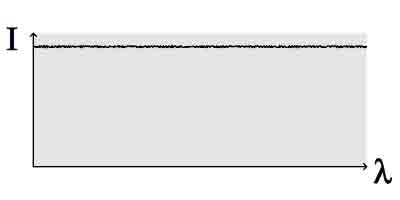Vous voyez ci-contre le spectre plat d'un bruit blanc (sur l'abscisse, la fréquence; en ordonnée, l'intensité)
Mais, nous direz-vous, jusqu'ici, on n'a somme toute fait que déplacer le problème et plus on explique et puis moins on comprend, bombardés que nous sommes par des termes plus obscurs les uns que les autres !
Il nous serait déjà utile d'avoir une idée de ce que l'on entend par "autocorrélation", non ? Hé bien : L'autocorrélation est un outil mathématique souvent utilisé en traitement du signal. C'est la corrélation croisée d'un signal par lui-même. L'autocorrélation permet de détecter des régularités, des profils répétés dans un signal comme un signal périodique perturbé par beaucoup de bruit, ou bien une fréquence fondamentale d'un signal qui ne contient pas effectivement cette fondamentale, mais l'implique avec plusieurs de ses harmoniques. Mais attention, car il y a une astuce : la confusion est souvent faite entre l'autocovariance et l'autocorrélation obtenue en divisant cette dernière par la variance. Ces deux notions généralisent les notions classiques de covariance ayant pour dimension la dimension de la variable élevée au carré et de coefficient de corrélation compris entre -1 et +1. Il existe d'autre part deux définitions fondamentalement différentes. À un processus stochastique discret ou continu, correspond une «autocorrélation» statistique qui généralise la notion de covariance. Dans le cas d'un processus continu (en toute généralité complexe)

Bruit blanc sonore

Le bruit blanc, à l'instar de la lumière blanche qui est un mélange de toutes les couleurs, est composé de toutes les fréquences, chaque fréquence ayant la même énergie. Le nombre de fréquences doublant d'une octave à l'autre, l'énergie croît linéairement de 3 dB par octave.

Notion de bruit blanc

Par analogie avec la lumière blanche qui contient toutes les fréquences lumineuses avec la même intensité, un bruit blanc est un processus stochastique qui possède la même densité spectrale de puissance à toutes les fréquences. Ceci correspond à une autocorrélation nulle en tout point sauf à l'origine : le processus est décorrélé. S'il est gaussien, cette décorrélation entraîne l'indépendance. La décorrélation conduit à une puissance moyenne ou variance infinie. Le processus correspondant ne peut donc exister mais c'est une approximation commode pour le calcul de la réponse d'un système peu amorti. Plus concrètement, un bruit blanc filtré à la fréquence fc correspond à un processus échantillonné à 1 / 2fc, ce résultat étant utilisé dans les simulations.

CONCLUSIONS PROVISOIRES

Nous pourrions poursuivre en évoquant le bruit blanc et ses solutions analytiques d'équations différentielles mais nous croyons avoir largement poussé le bouchon assez loin que pour démontrer à tout le moins que l'on pouvait continuer très longtemps d'investiguer ce domaine tout en le compliquant à l'infini dans les explications.
Il suffit de lire et de relire (au besoin) ce qui précède pour se rendre compte que le bruit blanc est donc une base relativement théorique et symbolique sur laquelle en fonction de certains facteurs, soit des interférences classiques peuvent intervenir et relever de l'accidentel, soit l'intervention d'énergies extérieures ou provoquées, sous toutes leurs formes ou presque, c'est-à-dire, plus simplement, qu'il s'agit d'un substrat potentiel à des communications parfaitement identifiées, mais également à toutes sortes d'autres communications éventuelles.

Tant de détours savants pour ça ? Hé bien oui, mais ces détours ne sont pas vains car ils démontrent scientifiquement que le bruit blanc n'est pas seulement un bruit comme tant d'autres, sans incidences particulières dans notre domaine. Cela a au moins pour conséquence d'attester que ce bruit blanc est bel et bien un "véhicule" possible de communications. Il ne s'agit donc pas d'une affirmation gratuite de la part de charlatans. Cela dit, n'allons pas trop vite en besogne non plus : cela n'atteste en aucune façon la réalité des communications prétendument en provenance de l'au-delà. En effet, s'il est possible d'analyser des sons enregistrés, c'est un autre problème que d'isoler une éventuelle communication et de l'identifier.

Cette petite investigation, qui se présente comme un pas de fourmi, est néanmoins très importante. Il convenait en effet de prendre le problème dès sa source. Si le bruit blanc ne pouvait résolument pas être un vecteur de TCI, il n'était pas utile d'aller plus loin. Nous venons de voir que tel n'était pas le cas, ce qui nous permettra de passer à l'étape suivante.

Mais avant cela, citons quand même une application du bruit blanc : le traitement des acouphènes. (Les acouphènes ? Non, ce ne sont pas des parasites ! L'acouphène est une impression auditive correspondant à la perception d'un son. Il s'agit de sensations sonores qui ne sont pas liées à une onde acoustique extérieure, c'est-à-dire qui sont seulement perçues par le sujet. Le son perçu ressemble à un bourdonnement, un sifflement ou même à un tintement ressenti dans le crâne ou dans l'oreille interne, d'un seul côté ou des deux. Il existe deux types d'acouphènes : l'acouphène objectif et l'acouphène subjectif. L'acouphène n'est pas une maladie mais un symptôme et ses causes sont nombreuses. Pour la petite histoire, disons que l'on peut ressentir un acouphène après une soirée passée dans une boîte de nuit, alors que le volume sonore est particulièrement important. Une fois que le silence revient, on perçoit alors un sifflement persistant dans l'oreille. Cela peut ne durer que quelques minutes mais aussi se prolonger pendant des heures. Cet exemple n'est qu'un cas d'acouphène très léger et passager, mais cela ne correspond en rien à ce que les personnes atteintes peuvent endurer. Les bruits décrits peuvent varier du rasoir électrique à la tondeuse à gazon ou même à l'avion à réaction, perçus en permanence, ou presque ! Dans ce cas, on comprend que les personnes atteintes d'acouphènes éprouvent un véritable calvaire dont les corollaires les plus évidentes sont les insomnies (et donc la fatigue très marquée), un stress important, des variations d'humeur très compréhensibles, etc.

SOMMAIRE - HAUT - ACCUEIL