Le nombre π et ses mystères
Qui n'a jamais séché sur les bancs de l'école, lorsque au cours de
maths, on passait à la géométrie, aux surfaces, aux volumes, etc. Ah ! Qu'est-ce que ce prof nous en faisait voir ! Et puis, avec son fameux π, la vache !
Il faut croire que de très nombreux élèves ont été confrontés à ce même genre de problème et depuis fort longtemps déjà. Mais de quand date le nombre π ? Quel est le
"scrôgneugneu" qui l'a inventé ? Et au fait, ce nombre a t'il une histoire ? C'est ce que nous allons voir !
Pour ce qui est de π... il y a bien pis !
Chacun sait (hum !), que le nombre π est bien utile, par exemple,
pour le calcul du périmètre d'un cercle, qui répond à la "douce poésie" suivante :
Périmètre d'un cercle = π X Diamètre du cercle, soit P = π X D
et le Périmètre d'un cercle = 2 X
π X Rayon du cercle soit P = 2 X π X R que l'on écrit : P = 2πR
π ( pi ) est le rapport constant entre la longueur d'un cercle (le périmètre
du cercle) et son diamètre (le double de son rayon).
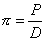 ou encore
ou encore 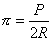
Voilà qui,
n'en doutons pas, vous comble de joie !
Seulement voilà, cela ne rend pas tout le monde
aussi heureux, à commencer par les mathématiciens
qui se trouvent embarrassés par ce type de
définition car en effet, elle ne fonctionne que si
l'on se réfère à un plan euclidien. Les choses ne se
comportent pas de la même manière si, par exemple,
on dessine un cercle sur une sphère, un ballon par
exemple.
Les mêmes mathématiciens préfèrent donc le type de
définition suivante, "beaucoup plus claire"...
(re-hum !)
On appelle pi et on note π
le double de l'unique racine de l'équation cos(x)
= 0, comprise entre 0 et 2.
( La fonction cos ayant été définie par )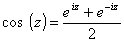
Ce qui est équivalent à :
π ( pi ) est le plus
petit nombre réel a > 0 tel que cos(a) = -1
Ou bien encore,
π ( pi ) est la moitié
de la période fondamentale de la fonction cosinus,
c'est-à-dire :
π est le plus petit
nombre réel a > 0 tel que

cos étant la fonction cosinus définie à
partir de la fonction exponentielle,
elle-même définie comme la somme d'une série entière
sur l'ensemble des nombres complexes...
Pour tout nombre complexe z,
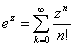 et et 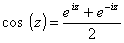 soit soit
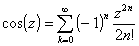
Et nous
supposons donc que, cette précision étant entendue,
vous dormirez désormais tranquilles à ce sujet.
L'histoire de π, où quand on va de π en π...
c'est de mieux en mieux !
 Avant toute chose, il
est bon de se rappeler que π vaut 3.141592654 (les décimales continuent
mais vous les connaissez aussi bien que nous...) Avant toute chose, il
est bon de se rappeler que π vaut 3.141592654 (les décimales continuent
mais vous les connaissez aussi bien que nous...)
Pour ceux qui s'inquiètent, à juste titre, de l'apparition de π sur
terre, disons que ce nombre est connu depuis la plus haute antiquité.
Pourtant, il faut y apporter une précision. En effet, s'il était connu
en tant que rapport entre la longueur du cercle et son diamètre et en
tant que méthode de calcul du périmètre du cercle ou de l'aire du disque
(que les Beatles ont révolutionnée, je sais !), en revanche, les gens de
cette époque ne connaissaient pas ce nombre comme notion abstraite de
constante mathématique).
Il faut dire aussi que ce n'est qu'en 1882 que
l'on a pu faire la démonstration de ce que π était un nombre
transcendant (solution à aucune équation à coefficients rationnels) et
puisque c'est Lindemann qui l'a dit...
Cela signifie, plus clairement,
que ce nombre n'est pas constructible à la règle et au compas. Autrement
dit, car j'en vois qui froncent les sourcils (là bas, dans le fond, à
côté du radiateur...), cela veut dire que si vous voulez coller
quelqu'un vous pouvez toujours lui proposer la quadrature du cercle.
Il s'agit d'un problème insoluble (quel que soit le liquide dans lequel
on le plonge). Cela consiste, si vous avez envie de vous amuser avec des
π, à construire un carré qui aurait la même aire qu'un disque de rayon
donné, mais en ne vous servant que des deux ustensiles cités plus haut.
En 2000 avant Jésus Christ, les Babyloniens connaissaient déjà π (mais
leur π était moins bon que le nôtre car il s'agissait d'une valeur
approchée (3.125). Pour eux, il s'agissait uniquement du rapport
constant entre la circonférence d'un cercle et son diamètre, mais ils
ignoraient l'objet mathématique (c'était le bon temps, quoi !). Comme les
Babyloniens calculaient en base 60
ils faisaient le calcul
suivant pour obtenir leur π tout en faisant de leur mieux :
3 + 7/60 + 30/3600, ou 3 + 1/8 = 3.125
Nous supposons que cette approximation devait avoir des conséquences
fâcheuses sur la tenue de route de leurs chars.
Aux alentours de 1650
avant notre ère, le papyrus de Rhind, écrit comme chacun sait par le
scribe Ahmès, possession d'un écossais du même nom (le papyrus, pas le
scribe) et conservé au British Museum, nous indique que les Égyptiens
connaissaient le nombre π, avec une valeur de 3.16, ce qui est déjà
mieux pour π. Ce papyrus est intéressant à plus d'un titre car il
constitue le plus vieux traité de mathématiques du monde, il comportait
quatorze feuilles et mesurait initialement plus de 5 mètres de long sur
32 cm de large. Son contenu dévoile déjà de grandes connaissances en
matière de calcul et pas seulement pour la construction de pyramides,
mais aussi pour le volume des greniers à grains, les aires planes,
l'arpentage, la décomposition des fractions, les équations...
NDLR : Les présentes
pages traitant de π ont été lues en classe de 6ème préparatoire de
l'Athénée Royal Jules Bordet de Soignies, par Mme Brancale (année
scolaire 2006-2007) et ont provoqué d'une part un fou rire général face
aux traits d'humour ici présents, d'autre part un intérêt accru des
élèves, lesquels se souviendront sans doute désormais de John Machin
(voir ci-dessous) et verront peut-être le
calcul de la circonférence du cercle avec moins de dé-π...
Merci à Mme Brancale !
Les π et autres Machins
Ce qui paraît assez
étrange, c'est la suite de l'évolution du nombre π et son apparition
dans le monde, surtout si l'on compare avec la valeur qu'on lui donnait.
Ainsi, π apparaît en Chine vers 1200 avant J.C. avec la valeur 3. Il est
assez étonnant que, 350 ans plus tard que les Égyptiens, les Chinois
aient "rétrogradé" dans l'approximation. Cela suppose donc que leur
découverte, pour importante qu'elle soit, ait été totalement
indépendante du reste du monde et qu'ils calculaient moins bien.
Néanmoins, nous supposons que l'on peut mettre l'indépendance en
question sur les difficultés de transport de l'époque. Mais, rebelote,
en 550 avant J.C., la Bible en parle, avec la même valeur, soit 3. Là,
les choses deviennent plus étonnantes encore quand on connaît les
accointances entre la Rome antique et l'Égypte. Ainsi donc, la belle
Cléopâtre n'aurait pas soufflé mot au bon Jules César de certaines
précisions capitales. Ah ! Les femmes !
Il faut encore attendre trois siècles pour que Archimède, entre deux
bains, donne l'encadrement 223/71 < pi < 22/7 en 250 avant J.C et que
Ptolémée en 150 utilise 3 +8/60 + 30/3600 = 3,1416666.
Mais revenons en Chine,
plus particulièrement au Ve siècle pour obtenir alors une valeur de π de
355/113 (il fallait le trouver aussi) ce qui donne : 3.14159292. On voit
qu'indéniablement la valeur s'affine pour π (phrase redoutable pour les
contrepèteries !) Mais les choses demeurent inégales puisque si l'on
consulte la situation en Inde, on voit que le 3.1416 est obtenu par 3 +
177/1250 mais en 380 et que, dans le coin, il faut attendre 640 pour que Brahmagupta atteigne les 3,16227 via la
racine carrée de 10, ce qui semble aussi une régression puisque 3.1416 -
π = 0.000007 et que 3.16227 - π vaut 0.0206. Heureusement pour lui,
disons quand même que, dans le chapitre 18 du Brahma-sphuta-siddhanta,
le savant traite des différentes opérations avec le zéro qu'il définit
comme le résultat de la soustraction d'un nombre par lui-même, des
nombres irrationnels, des équations quadratiques, des équations à
plusieurs inconnues et des solutions partielles d'équations du second
degré à deux inconnues. L'ouvrage atteindra Bagdad grâce à al-Fazari qui
le traduit en arabe vers 771 sous le titre de Al-Zij al-Sindhind
al-kabir. L'introduction de ces nouveaux concepts mathématiques aura une
grande répercussion sur la science dans le monde musulman des VIIIe et
IXe siècles.
Les choses commencent toutefois à progresser si l'on remonte le fil du
temps et que l'on s'en va d'abord au Moyen-Orient où Al Khwarizmi en 800
(en Ouzbekistan) et Al Kashi en 1429 (au Turkestan) calculent 14
décimales de π
Si on considère la situation en Europe, on retombe sur les mêmes
inégalités dans le savoir puisque. Fibonacci (retenez bien ce nom, qui,
nous en sommes sûrs, vous dit déjà quelque chose !), en 1220, trouve la
valeur 3,141818, que le Hollandais Van Ceulen trouve 20 décimales en
1596 puis 34 en 1609 !), tandis qu'en France Viète se contente de 9
décimales mais en 1593. On comprend mal, là aussi, cette différence
négative de 11 décimales dans la précision de π à trois années
d'intervalle et avec une telle proximité géographique. Faut-il en
conclure que tout le monde ne recevait donc pas "Sciences
et Vie" à l'époque ou qu'il y eut une grève des postes à ce
moment précis ?
Par la suite, l'intérêt
décroît en ce qui concerne l'évolution du nombre π car les techniques de
calcul se développent considérablement, notamment avec celui des
dérivées, des intégrales, et de toutes ces douceurs que l'on nous
servait à l'école et qui ont laissé une trace indélébile sur notre
sensibilité intra-moléculaire. Nous ne vous citerons donc plus les noms
des illustres π-onniers de la géométrie, sauf dans le cas bien précis
suivant, assez étonnant d'ailleurs, et qui méritait qu'on le signale : en
1706, c'est un certain "Machin" (ça ne s'invente pas et c'est
rigoureusement exact !) qui trouva 100 décimales au nombre en question !
John Machin est un mathématicien assez peu connu. Il est né en 1680 et
fut professeur d'astronomie à Londres. Il découvre en 1706 la formule
=16arctan(1/5)-4arctan(1/239), ce qui, grâce au développement en série
entière de arctan connu depuis Grégory, lui permet d'obtenir la formule
ci-dessus... Mais Machin a joué un grand rôle, d'abord parce que ce fut
le premier à calculer 100 décimales au moyen de sa formule, ce qui n'est
tout de même pas rien, mais surtout parce qu'il a ouvert la voie à la
recherche de formules d'arctan...
Plus récemment encore et à l'aide de procédés encore plus sophistiqués,
les frères Chudnovsky ont trouvé 4 milliards de décimales en 1994 et
Kanada et Tamura, dont le dernier record datait de 1999 avec 206
milliards de décimales ont fait mieux (du moins Kanada) le 6 décembre
2002 : 1 241 100 000 000 décimales. Mais, faut-il le dire (hé bien oui,
apparemment !), il s'agissait en fait d'un travail d'équipe, réalisé à
l'aide d'un calculateur (on aurait été surpris qu'il s'agisse d'un
micro-ondes) qui a duré 400 heures et cela malgré l'utilisation d'un
algorithme que l'équipe avait mis cinq ans à mettre au point.

John Machin
John Machin
(1680 -
1751) est connu principalement pour avoir calculé en
1706 100 décimales de pi grâce à la formule qui porte
son nom, la formule de Machin :
-
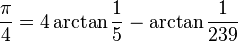
BiographieJohn Machin a enseigné les mathématiques à Brook Taylor en 1701, deux ans avant que
Taylor entre au St John's College (Cambridge). Il continua à correspondre avec lui pendant plusieurs années.
John a été ami avec Keill, qui enseigna à Oxford, et avec De Moivre qui a été comme Machin, un enseignant privé de mathématique en ce temps-là
Le 16 mai 1713, Machin a été nommé comme Professeur d'Astronomie au Gresham College à Londres. Il succéda au
Dr. Torriano et à continué à tenir la chaise jusqu'à sa
mort 38 ans plus tard.
John Machin a servi comme secrétaire de la Royal Society de 1718 à 1747. Il fit également partie de la commission qui décida de la priorité de
Calcul entre Leibniz et Newton en 1712.
En ce qui concerne la Formule de Machin établit en 1706, les intéressés pourront se servir des propriétés de la fonction arctan et noter
également que 120*239-119=119*239+120 pour tenter de la redémontrer
Œuvres
- The Laws of the Moon's Motion According to Gravity (1729)
- The solution of
Kepler's problem (1738)
- Quadrature of the Circle
(1758)
De
http://fr.wikipedia.org/wiki/John_Machin
NDLR: dixit Jonathan
Vanbockestal (fils de M. Vanbockestal, administrateur principal du
CERPI): "Si on pouvait calculer la circonférence d'un cercle comme on le
fait pour le périmètre d'un rectangle, soit avec LXl (longueur
multipliée par la largeur), on pourrait alors se dire : à quoi sert
π ? (à quoi CERPI ?)... lapsus révélateur !

|
